Chemistry & Matrices

Balancing Equations

We can use matrices to solve and balance chemistry equations.

Forexample if we have the following equation and we want to balance it. Its to easy, we use matrices.

                      

aFeCl₂ + bNa₃(PO₄)---> cFe₃(PO₄)₂ + dNaCl

The solution:

Fe: 1a + 0b -3c = 0d
Cl: 2a + 0b + 0c = 1d
Na: 0a + 3b + 0c = 1d
(PO₄): 0a + 1b - 2c = 0d

Note that you do not have a square matrix for Matrix A. Following the regular procedures, you should get a 4 x 3 matrix (four rows, three columns). You can make it square without changing the algorithm by adding a column of 1's at the end of the matrix

..

Very simple, very easy, it didnt take alot of time to balance it. so have fun and solve other equations with matrices!!!!!!  MATRICES MAKE YOUR LIFE EASIER AND MORE INTERESTING

Matrix Transforms

In applications that work with 3D graphics, you can use geometrical transforms to do the following:

• Express the location of an object relative to another object.
• Rotate and size objects.
• Change viewing positions, directions, and perspectives.

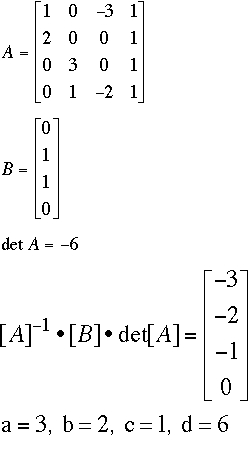
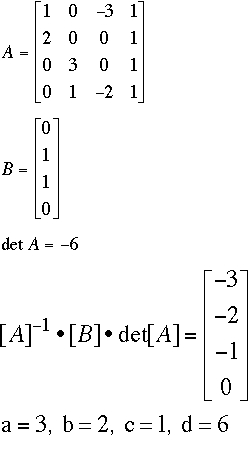
You can transform any point (x,y,z) into another point (x', y', z') by using a 4x4 matrix, as shown in the following equation.

Equation of transforming any point into another point

Perform the following equations on (x, y, z)

and the matrix to produce the point (x', y', z').

Equations for the new point

The most common transforms are translation, rotation, and scaling. You can combine the matrices that produce these effects into a single matrix to calculate several transforms at once. For example, you can build a single matrix to translate and rotate a series of points. Matrices are written in row-column order. A matrix that evenly scales vertices along each axis, known as uniform scaling, is represented by the following matrix using mathematical notation.

Liliane El Boueiz

Source: http://msdn.microsoft.com/en-us/library/bb206269(v=vs.85).aspx

Linear Algebra and Electricity

We must often analyze electric circuits such as the one shown to the right that cannot be described using the rules for resistors in series or parallel. The goal is to calculate the current flowing in each branch of the circuit or to calculate the voltage at each node of the circuit. We can use loop analysis or mesh analysis (which is a particular type of loop analysis) or nodal analysis to write down a system of equations describing the circuit. We can then use Gaussian elimination to solve this system of equations.

Loop analysis finds the currents directly and nodal analysis find the voltages directly. Which method is simpler depends on the given circuit. Knowing the branch currents, the nodal voltages can easily be calculated, and knowing the nodal voltages, the branch currents can easily be calculated. Nodal analysis is important because its answers can be directly compared with voltage measurements taken in a circuit, whereas currents are not so easily measured in a circuit (one must cut wires).

Reference: http://mathonweb.com/help/Theory.htm

A Video Screen is One Type of Matrix

A video screen is made up of tiny individual pixels (picture elements), each of which displays a specific color. On a computer monitor, the resolution of the screen is usually some size like 1024 pixels wide by 768 pixels high, or perhaps 800x600 or 640x480. On a television monitor (and in most conventional video images), the resolution of the screen is approximately 640x480, and on computers is typically treated as such. Notice that in all of these cases the so-called aspect ratio of width to height is 4:3. In the wider DV format, the aspect ratio is 3:2, and the image is generally 720x480 pixels. High-Definition Television (HDTV) specifies yet another aspect ratio—16:9.

Relative sizes of different common pixel dimensions

A single frame of standard video (i.e., a single video image at a given moment) is composed of 640x480="307,200" pixels. Each pixel displays a color. In order to represent the color of each pixel numerically, with enough variety to satisfy our eyes, we need a very large range of different possible color values.

There are many different ways to represent colors digitally. A standard way to describe the color of each pixel in computers is to break the color down into its three different color components —red, green, and blue ( a.k.a. RGB)—and an additional transparency/opacity component (known as the alpha channel). Most computer programs therefore store the color of a single pixel as four separate numbers, representing the alpha, red, green, and blue components (or channels). This four-channel color representation scheme is commonly called ARGB or RGBA, depending upon how the pixels are arranged in memory.

Jitter (small rapid variations in a waveform resulting from fluctuations in the voltage supply or mechanical vibrations or other sources) is no exception in this regard. In order for each cell of a matrix to represent one color pixel, each cell actually has to hold four numerical values (alpha, red, green, and blue), not just one. So, a matrix that stores the data for a frame of video will actually contain four values in each cell.

Each cell of a matrix may contain more than one number.

A frame of video is thus represented in Jitter as a two-dimensional matrix, with each cell representing a pixel of the frame, and each cell containing four values representing alpha, red, green, and blue on a scale from 0 to 255. In order to keep this concept of multiple-numbers-per-cell (which is essential for digital video) separate from the concept of dimensions in a matrix, Jitter introduces the idea of planes.

What is a Plane?

When allocating memory for the numbers in a matrix, Jitter needs to know the extent of each dimension—for example, 320x240—and also the number of values to be held in each cell. In order to keep track of the different values in a cell, Jitter uses the idea of each one existing on a separate plane. Each of the values in a cell exists on a particular plane, so we can think of a video frame as being a two-dimensional matrix of four interleaved planes of data.

The values in each cell of this matrix can be thought of as existing on four virtual planes.

Using this conceptual framework, we can treat each plane (and thus each channel of the color information) individually when we need to. For example, if we want to increase the redness of an image, we can simply increase all the values in the red plane of the matrix, and leave the others unchanged.

The normal case for representing video in Jitter is to have a 2D matrix with four planes of data—alpha, red, green, and blue. The planes are numbered from 0 to 3, so the alpha channel is in plane 0, and the RGB channels are in planes 1, 2, and 3.

Reference: http://www.cycling74.com/docs/max5/tutorials/jit-tut/jitterwhatisamatrix.html

Balancing Chemical Equations Using Matrices

Early on in your chemistry studies, you will have ample opportunity to balance equations! This is a fundamental skill in chemistry, as you might have noticed from the short reading in stoichiometry! Balancing equations means writing chemical equations such that the amount of stuff you start with in the reaction equals the amount of stuff you end up with as a product.
For example:

[A]Fe₂O₃ + [B]Al → [C]Al₂O₃ + [D]Fe

The blue letters represent the unknown coefficients to the balanced equation. To solve for these unknowns a system of equations must be generated. The easiest way to do this is to write a matrix relating the quantity of each element found in each reagent. The following table represents a break-down of this process, where each row represents a different element and each column represents an unknown coefficient. In this reaction there are 3 elements involved and 4 unknown coefficients.

	Fe2O3	+	Al	=	Al2O3	+	Fe
Fe	2		0		0		1
O	3		0		3		0
Al	0		1		2		0

Alternatively, this can be represented as a system of linear equations:

2A + 0B = 0C + 1D
3A + 0B = 3C + 0D
0A + 1B = 2C + 0D

Solve this system and you will easily get the answer !

Data retrieved from: http://www.personal.psu.edu/jzl157/balance.htm

The Application of Matrices to Business and Economics.

Problem:

Suppose that the economy of a certain region depends on three industries:

service, electricity and oil production. Monitoring the operations of these three industries

over a period of one year, we were able to come up with the following observations:

1- To produce 1 unit worth of service, the service industry must consume 0.3 units of its own production, 0.3 units of electricity and 0.3 units of oil to run its operations.

2-To produce 1 unit of electricity, the power-generating plant must buy 0.4 units of

service, 0.1 units of its own production, and 0.5 units of oil.

3-Finally, the oil production company requires 0.3 units of service, 0.6 units of

electricity and 0.2 units of its own production to produce 1 unit of oil.

Find the production level of each of these industries in order to satisfy the external and the internal demands assuming that the above model is closed, that is, no goods leave or enter the system.

Solution:

Consider the following variables:
1. p1= production level for the service industry
2. p2= production level for the power-generating plant (electricity)
3. p3= production level for the oil production company

Since the model is closed, the total consumption of each industry must equal its total

production. This gives the following linear system:

0.3p1 + 0.3p2 + 0.3p3 = p1

0.4p1 + 0.1p2 + 0.5p3 = p2

0.3p1 + 0.6p2 + 0.2p3 = p3

The input matrix is:

A=

0.3 0.3 0.3

0.4 0.1 0.5

0.3 0.6 0.2

and the above system can be written as (A-I)P=0. Note that this homogeneous system has infinitely many

solutions (and consequently a nontrivial solution) since each column in the coefficient matrix sums to 1. The

augmented matrix of this homogeneous system is :

-0.7 0.3 0.3 0

0.4 -0.9 0.5 0

0.3 0.6 -0.8 0

which can be reduced to :

1 0 -0.82 0

0 1 -0.92 0

0 0 0 0

To solve the system, we let p3 =t (a parameter), then the general solution is :

p1= 0.82t

p2=0.92t

p3=t

The values of the variables in this system must be nonnegative in order for the model to make sense. In other words, t ≥ 0. Taking t=100 for example would give the solution :

p1= 82 units

p2= 92 units

p3= 100 units.

I chose an example of real life problem related to economics that shows how matrices can be effective and helpful when it comes to solving complicated problems. Matrices let us arrange numbers and get solutions to our problem in a quick and easy way !

Matrices used in physics

USE OF MATRICES IN STUDYING OPTICAL SYSTEM
Matrix approach helps understand how optical system works.Optical system has an input plane and output plane. Ray of light is determined by the distance that hits above or below the object axis and the slope of light r’.
Develop a working model-Ray matrices : Newtonian or Gaussian optics tell you where all rays that start from some object point will meet again to form an image (massively parallel). They tell you nothing about what rays are doing at points in the system that are not object or image points. This is a very useful approach for calculating images position and magnifications in the paraxial limit.
Ray matrices tell you the position and the slope of a single ray at a single plane (serial). The ray matrix approach is more flexible but serial rather than parallel ans is very well suited to using computers.

How to proceed?
We find the matrix to each element that comprise the optical system.
[M1], [M2], [M3], [M4], [M5].
[M1]=
[M2]= etc…
We multiply them together to get a single matrix. We multiply them in reverse order because the ray comes on the input plane first. Like this we find the ray matrix that helps us know what happens at every ray in the each plane

.
Reference: http://www.youtube.com/watch?v=DLF5acjI51Q

Cryptography With Matrices

The ciphers used in cryptograms were originally created for real encryption of military or personal secrets. The word cryptogram is derived from the Greek word Kryptos meaning hidden and Gramma meaning letter. The first use of the cryptogram for entertainment purposes occurred during the Middle Ages by monks who had spare time for intellectual games. The goal is to take a message and encrypt it into a string of numbers via matrix multiplication. The receiving party then has to take the string of numbers and decrypt it back to the original message.
How?
As an initial example, we shall use the following message:

"HI THERE BUDDY"

I- Alpha-Numeric Substitution
First, we must assign each letter a numeric equivalent. Here, we shall reserve the number 0 to represent a space and use the numbers 1 – 26 to represent the 26 letters. Rather than just making a direct substitution in order, we can permute the digits in some way.

For example:

II- Coding Matrix
Choose an invertible n x n matrix A, for some size n , which will be used to encrypt the message. For example:

III- Encrypting the Message
We first convert the message above into the numeric script, using the alpha-numeric Substitution set in Step I: (H = 7, I = 10, Blank = 0, etc).
HI THERE BUDDY is then 7 10 0 19 7 6 17 6 0 1 22 3 3 26
Then we convert this script into a m x n matrix (n columns because our A is n x n).
The number of rows m depends on the length of the message.

We fill out the last row with more 0's as necessary:

Now Let C be the encrypted code of the original message. C = B * A.

Finally, we convert matrix C into a string that becomes the following encrypted message:
–39 –36 –19 69 51 71 15 4 27 –102 –84 –64 –147 –124 –95

IV- Decrypting the message
The second party receives only the encrypted message above. However the receiver knows the alpha-numeric code (Step I) and the coding matrix A (Step II). Thus, the encrypted script is converted back into an m x n matrix C and then multiplied by the inverse of A (A-1) to undo the original matrix multiplication.
C = B * A, then B = C * A-1 .

The result matrix is then converted back to the alphabet.

************************************

For further explanation, and different examples, follow the link below:

http://docs.google.com/viewer?a=v&q=cache:WvLXDcuAVeUJ:guilford.rps205.com/departments/math/Links/Algebra%2520II%2520-%2520College%2520Alg/4.4%2520Cryptograms%2520Using%2520Inverse%2520Matrices%2520in%2520Real%2520Life.ppt+Using+matrices+in+real+life+situations&hl=en&gl=lb&pid=bl&srcid=ADGEEShGe_l27hVpKU9ZAe2Rzu-E0o7jFV92YM4J8MBy45fH-6CbGTMpVvuwwU8VjYjAG3E-UvF5tnEJcKSLufILXu6t7rU4q-fCaxbuEL-ZJBxqM3FkvzYxMA9mwWO4y1BaqSng-FIO&sig=AHIEtbT643q6cCFdi7WwYXBsTsQGJM7OaQ

**********************************

And now, here is my encrypted message for you all.
Decrypt it and comment on my post including what you figure it out to be:

144 124 118 -111 -100 -59 186 162 150 174 144 152 !!!

The Decision Matrix: Buying a Car

Use a decision matrix to compare criteria and identify the choice that best meets your neds.

By Ted Mitchell
Published January 10, 2007

Ideas

In the pages of Raise the Hammer, any implied approval of cars might go over as blasphemy; but my primary purpose here is to demonstrate the process of using an engineering decision matrix to address a common problem: how to buy a car that best meets your needs.

Several sources will give you their take on car comparisons, but you can do it yourself using only those criteria which matter to you.

In 2002, Toyota revived the hatchback class with the Matrix. Seeing wildly successful sales numbers, other manufacturers quickly jumped in. These cars are small on the outside, large on the inside, offer reasonable price, safety, fuel economy and practicality.

That is, they provide actual sport and utility, unlike the traditional concept of the euphemistically named SUV. Think Meadowlands, you get the idea.

Maybe one of these is for you, but they are all so similar - how does one make sense of it? Like most people, you could buy on price - or reputation, impulse, colour, shape, or (chuckle) how well your desired self-image fits with those people seen in the commercials.

Decision Matrix

To make an intelligent decision, you should use a decision matrix.

First, compile a list of things relevant to you. For example: power, fuel economy, price, safety, reliability, cargo capacity, and the ability to hold your two teenagers comfortably.

Next, pick specifications that are available and will quantify those qualities.

Set Criteria

The first iteration is to refine the criteria. For example, power by itself doesn't do much if the vehicle is heavy. What you really want is a measure of acceleration.

This is actually tested by performance magazines, but you can't find numbers for all the cars you are interested in. Instead, approximate by dividing horsepower by vehicle weight. You now have Criteria 1: Power to Weight Ratio.

Fuel economy ratings are available from Transport Canada. Your use splits city and highway ratings 50:50. This is Criteria 2: Average Fuel Economy.

How well do the teenagers fit? The best measure is rear legroom, an often compromised dimension. Criteria 3:Rear Legroom.

Cargo capacity is a tough one because companies list many incomparable figures. The only statistic available for all is trunk volume with seats up; Criteria 4: Cargo Capacity. Note, however, that total volume with seats folded does not correlate well with this.

Safety ratings can be found from crash testing. NHTSA has a listing of frontal driver, passenger, side front and rear impacts, as well as rollovers, all out of five stars. All numbers are average them for each vehicle. This givesCriteria 5: Safety Rating.

Reliability data is a bit elusive, especially for such a new segment. Consumer Reports uses a five division system for predicted reliability, and where they have no information, use data for the closest similar model. VoilaCriteria 6: Predicted Reliability.

Last but not least, delivery and all-taxes-in Criteria 7: Purchase Price.

Choose Vehicles

Next, choose the vehicles. You should include as many as possible, but let us limit them to a certain rough size, deciding on constraints (features that you must have) of four doors, automatic transmission, ABS, air conditioning, and side airbags.

Pick trim packages that have most features in common.

I have chosen the following five: Honda Fit, Mazda 3 Sport, Nissan Versa, VW Rabbit, and a unibody SUV, the Ford Escape (2WD version). Here are the numbers:

Table 1: Raw Data

Automobile	Honda Fit LX	Nissan Versa SL CVT	VW Rabbit 5 door	Mazda 3 Sport GS	Ford Escape XLS FWD
hp	109	122	150	156	153
wt (kg)	1143	1261	1423	1338	1479
power/weight	0.095	0.097	0.105	0.117	0.103
l/100k city	7.8	7.9	10.5	9.4	10.4
l/100k hwy	5.6	6.1	7.1	6.9	8.4
avg l/100k	6.7	7	8.8	8.15	9.4
rear legroom (mm)	856	966	896	922	922
cargo up (L)	603	504	400	484	830
cargo down (L)	1186	1427	?	884	1877
Safety Stars
driver frontal	5	4	4	4	4
pass frontal	5	4	4	4	4
front side	5	5	5	3	5
rear side	3	5	5	3	5
rollover	4	4	4	4	3
average	4.4	4.4	4.4	3.6	4.2
reliability stars	5	3	1	4	3
total price	22350	22460	26492	28265	32567

Note that our prototype, the Toyota Matrix, fails the constraint requirement of ABS and side airbags. Remember that imposing too many constraints is foolish: you will not consider vehicles that otherwise will meet your criteria nicely.

Normalize and Weight the Data

Now, we need to do two more things.

First, normalize the data for ease of comparison. That is, give the highest rank a value of 1 and everything else is divided by that value to give a fraction between zero and 1.

Second, multiply the quantities by a factor which corrects for the relevance of the quantity.

Most of our factors do not need adjustment, but look at legroom: the smallest and largest differ only by 11 percent. If your kids' legs require something in between, this is the difference between very cramped and lots of room.

To make this figure relevant, let's expand by a factor of three. Mathematically, that equals (Value x 3) ? 2.

Also, we need to invert price, as less expensive is the desired outcome. Similarly, we could have adjusted the relative reliability data to have a less severe rating, or simply adjust for this later in the weighting below.

Table 2: Normalized Criteria Rating

	Fit LX	Versa 5L CVT	Rabbit 5 door	Mazda 3 GS	Escape XLS FWD
power/wt	0.82	0.83	0.90	1.00	0.89
avg fuel economy	1.00	0.96	0.76	0.82	0.71
legroom adjusted	0.66	1.00	0.78	0.86	0.86
cargo cap'y	0.73	0.61	0.48	0.58	1.00
safety rating	1.00	1.00	1.00	0.82	0.95
reliability	1.00	0.60	0.20	0.80	0.60
price (inverted)	1.00	1.00	0.84	0.79	0.69

Finally, weight the relative importance of each criterion. Up to now, the choices have been fairly universal. But this step is entirely your choice. The simplest way is to give equal weight. We will use this:

Table 3: Relative Importance by Criterion

Measure	Weight
Power to Weight ratio	10%
Average Fuel Economy	15%
Rear Legroom	10%
Cargo Capacity	15%
Safety Rating	20%
Predicted Reliability	10%
Purchase Price	20%

Now we can multiply each weight by each rating, then add the results to produce a total score and rank.

Table 4: Results

	Weight %	Fit LX	Versa 5L CVT	Rabbit 5 door	Mazda 3 GS	Escape XLS FWD
power/wt	10	8.2	8.3	9.0	10.0	8.9
avg. fuel econ	15	15.0	14.4	11.4	12.3	10.7
legroom	10	6.6	10.0	7.8	8.6	8.6
cargo	15	10.9	9.1	7.2	8.7	15.0
safety	20	20.0	20.0	20.0	16.4	19.1
reliability	10	10.0	6.0	2.0	8.0	6.0
price	20	20.0	19.9	16.9	15.8	13.7
total score	100	90.7	87.7	74.4	79.9	82.0
Rank		1	2	5	4	3

Note that different weightings may produce different rankings. An emphasis on cargo would favour the Ford. Acceleration, the Mazda. Economy, the Honda. Legroom, the Nissan.

There is no weighting which favours the VW. It would take a different set of criteria to get the Rabbit off the ground.

If subjective factors are used such as ride quality and noise, this misses the whole point of using objective, quantifiable criteria.

However, some of these "soft" factors can be significant but are highly prone to marketing suggestion and bias; for example, the good reputation perhaps undeservedly enjoyed by VW in this country.

The next time you need to make an informed, objective decision, have a go at the decision matrix. Or, you can pay the stupid tax.