Since a 2 x 2 matrix corresponds uniquely to a linear transformation from R² to R², we can think of a matrix as transforming a planar figure into a new planar figure.

Example

Consider the matrix

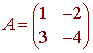
and the triangle with vertices (0,0), (12), (5,3). We have

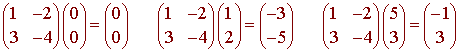
It is a property of linear transformations that if the matrix is nonsingular, then line segments map onto line segments. Hence triangles map onto triangles. The picture below shows the original triangle.

---

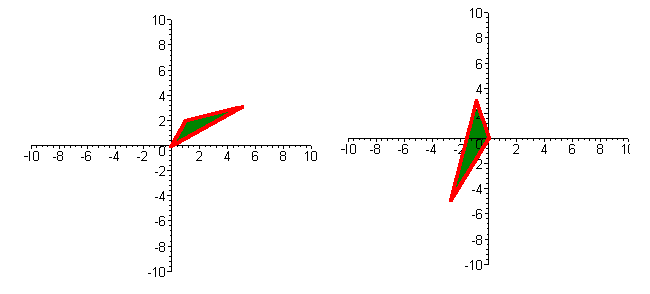
Some Basic Transformations

There are certain basic transformation that are building blocks for general transformations.

Example Reflection With Respect to the x axis.

To find the matrix for this transformation, we consider where the vectors e₁ and e₂ are mapped. The reflection with respect to the x-axis makes the y-coordinate negative and leaves the x-coordinate constant. We have

L(1, 0) = (1, 0) L(0, 1) = (0, -1)

These vectors are the column vectors for the matrix. We have

---

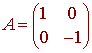
Example Reflection About the Line y = x

We see that

L(1,0) = (0,1) L(0,1) = (1,0)

so that

---

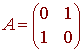
Example Rotation About an Angle q

The point (0,1) rotated about this angle is on the unit circle at radian angle q. The point (1,0) rotated about this angle is on the unit circle at radian angle p/2 + q. We have

L(1,0) = (cos q, sin q) L(0,1) = (cos(p/2 + q), sin(p/2 + q) = (-sin q, cos q)

We have

---

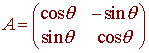
Example Shear in the y-direction

Another transformation that is common in computer graphics is a shear in the x or y direction. The picture below gives and example

The matrix that makes this happen is

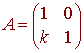
for some constant k.